Publications
My published scientific work spans numerous domains. So at first glance, it might seem disjoint or disparate.
But this is actually incorrect—all of my work here is part of the same ongoing project, or process,
as fundamental connections exist therein.
As I stand upon the shoulders of giants and wield the methods of science and mathematics,
my intent is to continue to develop, explore, and strengthen my work, and related work, as we blast towards a transcendant goal:
onwards to unification my friends!
A scientist's work is never complete. A warrior never surrenders.
Update [October 2025]:
I'm back in action after taking an 8-year pause from science due to important life events.
I'm currently operating in "late night hobby mode" due to full time work and other things, but
I just finished my *third* preprint (this year) after coming back.
Two of these preprints are being reviewed by journals and
I'm preparing my latest preprint for submission to a journal.
More to come!
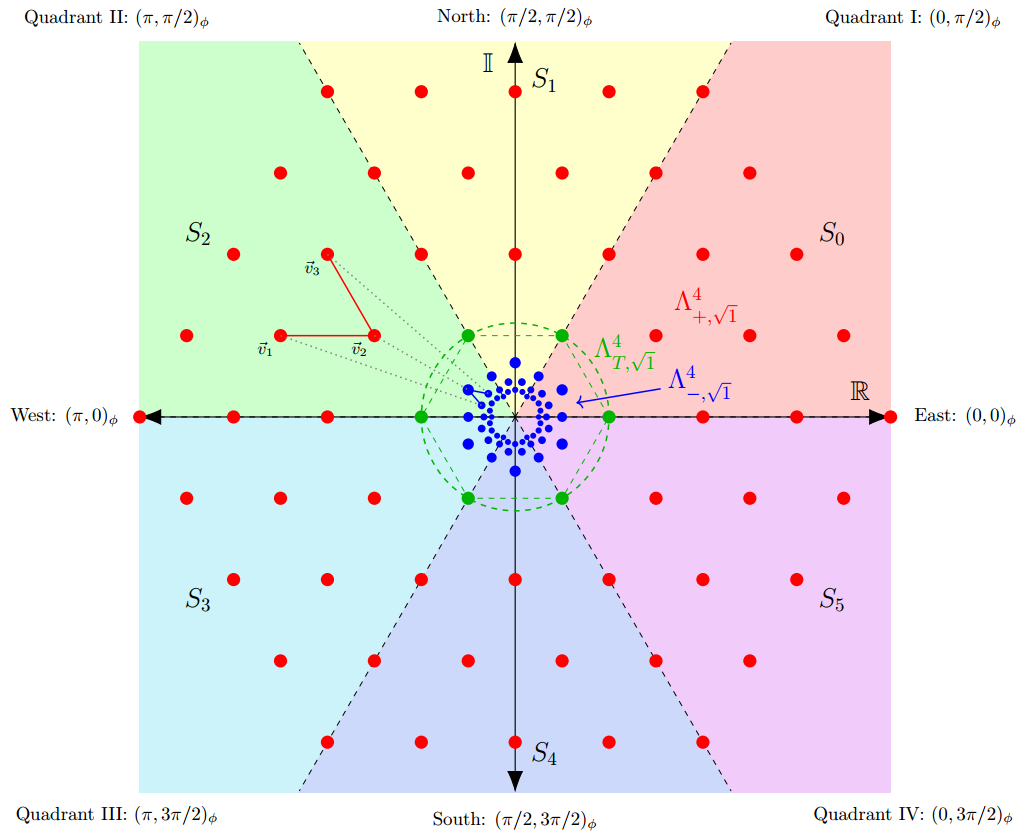
The Tri-Quarter Framework: Radial Dual Triangular Lattice Graphs with
Exact Bijective Dualities and Equivariant Encodings via
the Inversive Hexagonal Dihedral Symmetry Group 𝕋24
Status: Preparing for a journal submission
September 26, 2025
Nathan O. Schmidt
The Tri-Quarter framework unleashes a radial dual triangular lattice graph with
unified complex-Cartesian-polar coordinates, structured orientation phase pair assignments
for directional labeling, and topological zones to build exact bijective mappings without
approximations. By establishing combinatorial duality for radial separation, Escher
reflective duality for zone swapping, and bijective self-duality for reversible transformations,
the discretized framework leverages the lattice graph's order-6 rotational symmetry to natively
support angular sectors, modular decompositions, equivariant encodings, and trihexagonal
six-coloring for conflict-free parallel algorithms. At this discretized framework's core is
the Tri-Quarter Inversive Hexagonal Dihedral Symmetry Group 𝕋24—the order-24 semidirect
product D6 ⋊ ℤ2—which exploits rotational, reflective, and inversive symmetries to unlock
these bijective transformations with exact precision. We provide formal proofs of these
dualities, along with numerous step-by-step examples, and demonstrate practical efficiency
through benchmarked simulations to achieve ~2x speedups with inversion-based path mirroring
via bijections and up to ~6x reductions in symmetry-reduced clustering via rotational orbits.
This work advances scalable computations on symmetric structures, with applications in
computational geometry, graph traversals, tiling, robotics path planning,
multi-agent coordination, lattice-based cryptography, image processing, and signal processing.
This work aims to solidify a mathematical and computational foundation for
both classical and non-classical computing paradigms—targeting future integrations in
complex emergent systems that harness intricate “superposition-like” symmetries to
advance symmetry-aware algorithms and data structures across diverse computing architectures.
Tri-Quarter Framework Case Study: BPSK Signal Processing
Status: Being reviewed at a journal
July 4, 2025
Nathan O. Schmidt
In this case study, we engage the novel Tri-Quarter framework
by applying it to Binary Phase-Shift Keying (BPSK) signal processing,
where we leverage structured orientation phase pair assignments and
dynamic weight adjustments to enhance noise filtering and error correction
under Gaussian and non-Gaussian noise. We address the challenge of reliable decoding
in communication systems like wireless networks, satellite links, and IoT devices,
where noise varies from Additive White Gaussian Noise (AWGN) to impulsive noise (IN)
interference. The framework implements a model-free methodology by using sign-based
phase assignments and distance-based weights to decode signals without prior noise
knowledge. Simulations at a signal-to-noise ratio (SNR) of 6 dB with 100,000 trials
demonstrate that the Tri-Quarter framework's noise filtering achieves a 2.350%
bit error rate (BER) in AWGN, closely matching standard thresholding with 1 CPU cycle,
while its error correction with 3 transmissions per symbol yields a 0.138%
BER in AWGN and 0.430% BER in IN, performing comparably to majority voting
(0.149% BER in AWGN, 1.415% BER in IN) and significantly outperforming
Gaussian-tuned soft-decision decoding (0.030% BER in AWGN, 12.769% BER in IN)
in non-Gaussian conditions. With 17 CPU cycles for error correction,
the Tri-Quarter framework balances efficiency and robustness, dominating in
unpredictable noise environments (e.g., urban cellular wireless networks,
industrial IoT networks, oceanographic sensor networks, and naval communication networks),
though it is less optimal for ultra-low-power devices or Gaussian-dominated environments.
This framework offers a versatile solution for modern communication challenges, with
potential extensions to complex modulations like Quadrature Phase-Shift Keying (QPSK).

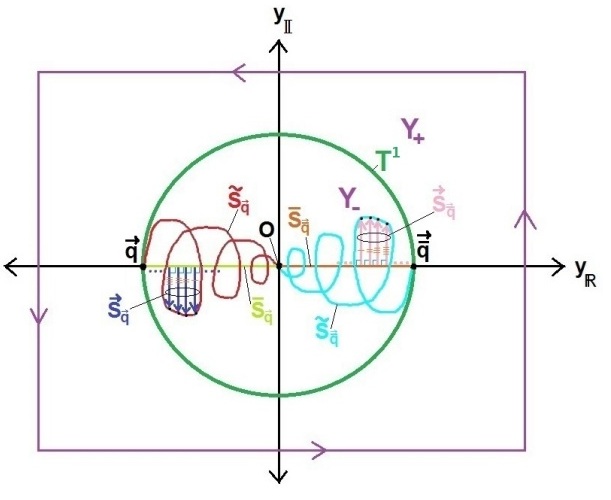
The Tri-Quarter Framework: Unifying Complex Coordinates with Topological and Reflective Duality
across Circles of Any Radius
Status: Being reviewed at a journal
June 13, 2025
Nathan O. Schmidt
In this paper, we introduce the Tri-Quarter Topological Duality Theorem,
the foundation of a novel mathematical framework that unifies complex, Cartesian,
and polar coordinate systems on the complex plane ℂ while equipping the
circle Tr of radius r > 0 with a new topological property.
Our framework integrates a generalized coordinate system—where real and
imaginary components are assigned unique phase pairs—with a structured
orientation that elevates Tr to an active separator with intrinsic
directional properties. We prove that Tr, as the boundary zone,
exhibits topological duality with the inner zone X-,r (||x|| < r)
and outer zone X+,r (||x|| > r),
ensuring consistent separation between inner and outer radial directions across
Tr with a phase pair map encoding additional information.
We also introduce the Escher Tri-Quarter Reflective Duality Theorem,
proving reflective duality across Tr via a circle inversion map
that preserves phase pairs while swapping X-,r and X+,r.
Moreover, these phase pair assignments provide a combinatorial classification of
directional structures in ℂ, enhancing the topological analysis.
This approach offers insights into topological separation, orientation, and
reflection, facilitating analysis of systems with circular symmetry, with
potential applications in fields such as black hole physics, signal processing,
and other areas reliant on complex domain partitioning.
A case study on quadrant-based transformations demonstrates streamlined
directional mappings, geometric elegance, unified classification, and
computational efficiency in ℂ. For instance, in the case study,
the Tri-Quarter approach consistently reduces the number of comparison
conditional checks from a maximum of 7 in the standard method to a maximum of 4,
significantly enhancing computational efficiency.
A software tool visualizes some of these concepts, with future work aimed at
exploring practical implementations.

Interferometric Detection of Gravitational Waves: How can a Wild Roam Through Mindless Mathematical
Laws Really be a Trek Towards the Goal of Unification?
FQXi • Wandering Towards a Goal Essay Contest 2016-2017
March 6, 2017
Christian Corda Reza Katebi Nathan O. Schmidt
The event GW150914 was the first historical detection of gravitational waves (GWs).
The emergence of this ground-breaking discovery came not only from incredibly innovative
experimental work, but also from a centennial of theoretical analyses. Many such analyses
were performed by pioneering scientists who had wandered through a wild territory of mathematical
laws. We explore such wandering and explain how it may impact the grand goal of unification
in physics.
Latin Squares and Their Applications to Cryptography
Boise State University Theses and Dissertations
Number 1223
December 1, 2016
Nathan O. Schmidt
A latin square of order-n is an n-by-n array over a set of n symbols such that every symbol appears
exactly once in each row and exactly once in each column.
Latin squares encode features of algebraic structures.
When an algebraic structure passes certain "latin square tests", it is a candidate for use in the
construction of cryptographic systems.
A transversal of a latin square is a list of n distinct symbols, one from each row and each column.
The question regarding the existence of transversals in latin squares that encode the Cayley tables
of finite groups is far from being resolved and is an area of active investigation.
It is known that counting the pairs of permutations over a Galois field Fpd whose point-wise sum
is also a permutation is equivalent to counting the transversals of a latin square that encodes the
addition group of Fpd.
We survey some recent results and conjectures pertaining to latin squares and transversals.
We create software tools that generate latin squares and count their transversals.
We confirm previous results that cyclic latin squares of prime order-p possess the maximum transversal
counts for 3 ≤ p ≤ 9.
Furthermore, we create a new algorithm that uses these prime order-p cyclic latin squares as
"building blocks" to construct super-symmetric latin squares of prime power order-pd with d > 0;
using this algorithm we accurately predict that super-symmetric latin squares of order-pd possess
the confirmed maximum transversal counts for 3 ≤ pd ≤ 9 and the estimated lower bound on the maximum
transversal counts for 9 < pd ≤ 17. Also, we give some conjectures regarding the number of transversals
in a super-symmetric latin square.
Lastly, we use the super-symmetric latin square for the additive group of the Galois field (F32, +)
to create a simplified version of Grøstl, an iterated hash function, where the compression function is
built from two fixed, large, distinct permutations.

Confusion in Cosmology and Gravitation
International Journal of Theoretical Physics
Volume 55 • Number 10 • Page 4331
June 13, 2016
Christian Corda Reza Katebi Nathan O. Schmidt
In a series of papers, Santilli and collaborators released various strong statements against the
general theory of relativity (GTR) and the standard λCDM model of cosmology. In this paper we show that such
claims are due to misunderstandings of basic concepts of gravitation and cosmology. In particular, we show that
Santilli and collaborators demonstrated neither that the GTR is wrong, nor that the Universe is not expanding.
We also show that the so-called iso-gravitation theory (IGT) of Santilli is in macroscopic contrast with geodesic
motion and, in turn, with the Equivalence Principle (EP) and must therefore be ultimately rejected. Finally,
we show that, although the so called iso-redshift could represent an interesting alternative (similar to the
tired light theory historically proposed by Zwicky) to the Universe expansion from a qualitative point of view,
it must be rejected from a quantitative point of view because the effect of iso-redshift is 10-6 smaller than
the effect requested to achieve the cosmological redshift.

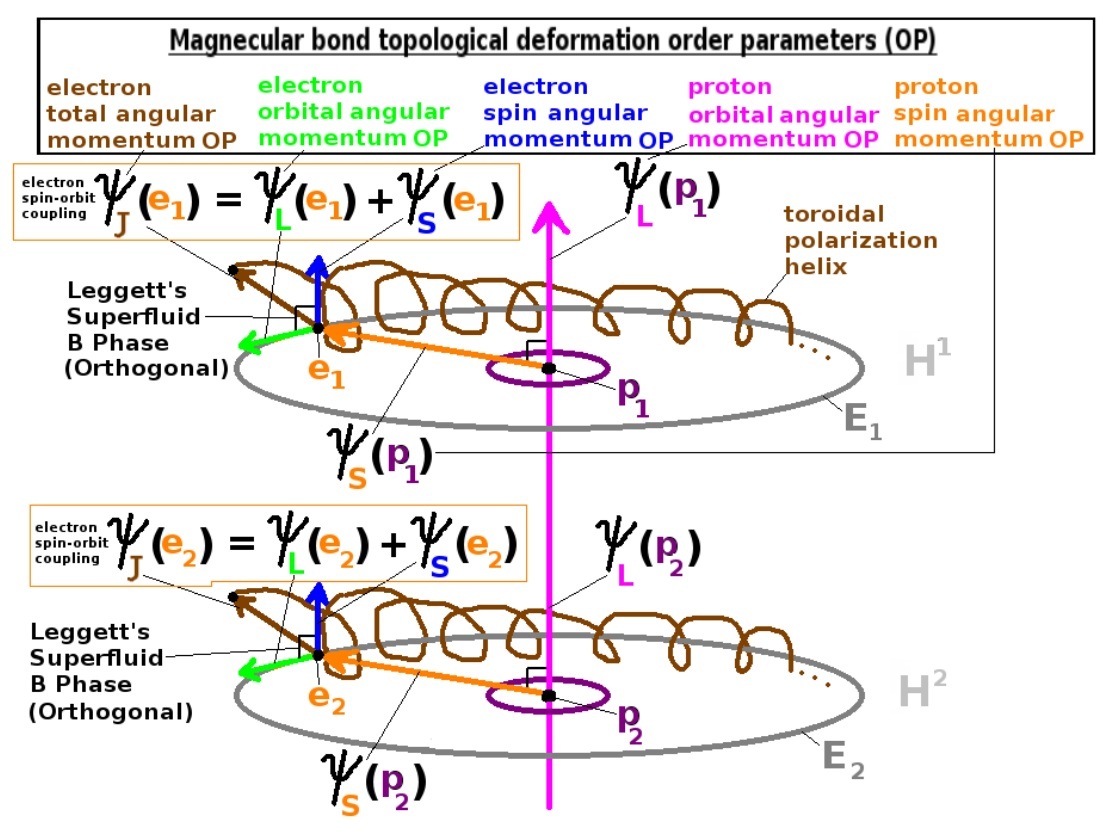
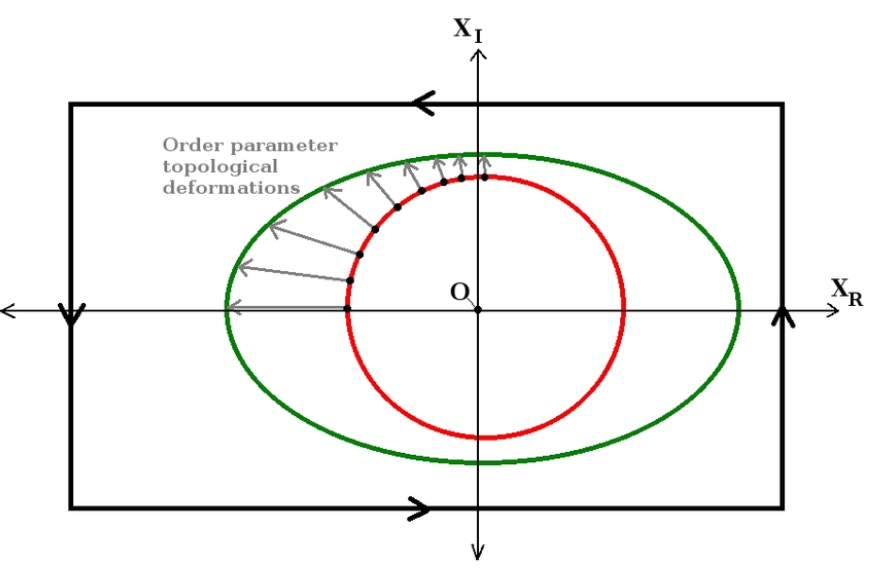
A Brief Note on the Magnecule Order Parameter Upgrade Hypothesis
AIP Conference Proceedings: 2014 ICNAAM at Rhodes, Greece
Volume 1648 • Issue 1 • Page 510016
March 10, 2015
Nathan O. Schmidt
In this short remark, we report on recent hypothetical work that aims to equip Santilli's magnecule model
with topological deformation order parameters (OP) of fractional statistics to define a preliminary set of
wave-packet wave-functions for the electron toroidal polarizations. The primary objective is to increase the
representational precision and predictive accuracy of the magnecule model by exemplifying the fluidic
characteristics for direct industrial application. In particular, the OPs are deployed to encode the
spontaneous superfluidic gauge symmetry breaking (which may be restored at the iso-topic level) and
correlated with Leggett's superfluid B phases to establish a long range constraint for the wave-functions.
These new, developing, theoretical results may be significant because the OP configuration arms us with an
extra degree of freedom for encoding a magnecule's states and transitions, which may reveal further insight
into the underlying physical mechanisms and features associated with these state-of-the-art magnecular bonds.
Launching the Chaotic Realm of Iso-Fractals: A Short Remark
AIP Conference Proceedings: 2014 ICNAAM at Rhodes, Greece
Volume 1648 • Issue 1 • Page 510017
March 10, 2015
Nathan O. Schmidt Reza Katebi Christian Corda
In this brief note, we introduce the new, emerging sub-discipline of iso-fractals by highlighting and
discussing the preliminary results of recent works. First, we note the abundance of fractal, chaotic,
non-linear, and self-similar structures in nature while emphasizing the importance of studying such
systems because fractal geometry is the language of chaos. Second, we outline the iso-fractal generalization
of the Mandelbrot set to exemplify the newly generated Mandelbrot iso-sets. Third, we present the
cutting-edge notion of dynamic iso-spaces and explain how a mathematical space can be iso-topically
lifted with iso-unit functions that (continuously or discretely) change; in the discrete case examples,
we mention that iteratively generated sequences like Fibonacci’s numbers and (the complex moduli of)
Mandelbrot’s numbers can supply a deterministic chain of iso-units to construct an ordered series of
(magnified and/or de-magnified) iso-spaces that are locally iso-morphic. Fourth, we consider the
initiation of iso-fractals with Inopin’s holographic ring (IHR) topology and fractional statistics
for 2D and 3D iso-spaces. In total, the reviewed iso-fractal results are a significant improvement
over traditional fractals because the application of Santilli’s iso-mathematics arms us an extra
degree of freedom for attacking problems in chaos. Finally, we conclude by proposing some questions
and ideas for future research work.

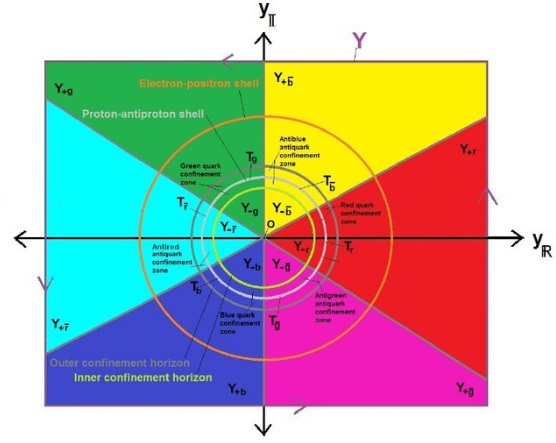
Launching the Six-Coloring Baryon-Antibaryon Antisymmetric Iso-Wavefunctions and Iso-Matrices
Hadronic Journal
Volume 37 • Number 5 • Page 503
October 1, 2014
Nathan O. Schmidt
In this work, we upgrade the Inopin-Schmidt quark confinement and baryon-antibaryon duality
proof with Santilli's new iso-mathematics. For a baryon-antibaryon pair confined to the six-coloring
kagome lattice of the Inopin Holographic Confinement Ring (IHCR), we construct a cutting-edge procedure
that iso-topically lifts the antisymmetric wavefunctions and matrices to iso-wavefunctions and iso-matrices,
respectively. The initial results support our hypothesis that transitions between the energy and resonance
states of the hadronic spectra may be rigorously characterized by properly-calibrated iso-topic liftings.
In total, these rich developments suggest a promising future for this emerging iso-confinement framework,
which must be subjected to additional scientific inquiry, scrutiny, and exploration.
Toward a Topological Iso-String Theory in 4D Iso-Dual Space-Time: Hypothesis and Preliminary Construction
Hadronic Journal
Volume 37 • Number 5 • Page 585
October 1, 2014
Nathan O. Schmidt
We propose a preliminary framework that engages iso-triplex numbers and deformation order parameters to
encode the spatial states of Iso-Open Topological Strings (Iso-OTS) for fermions and the temporal states
of Iso-Closed Topological Strings (Iso-CTS) for bosons, where space and time are iso-dual. The objective
is to introduce an elementary Topological Iso-String Theory (TIST) that complies with the holographic
principle and fundamentally represents the twisting, winding, and deforming of helical, spiral, and vortical
information structures—by default—for attacking superfluidic motion patterns and energy states with
iso-topic lifting. In general, these preliminary results indicate a cutting-edge, flexible, consistent,
and powerful iso-mathematical framework with considerable representational capability that warrants further
examination, collaboration, construction, and discipline.
Effective Dynamic Iso-Sphere Inopin Holographic Rings: Inquiry and Hypothesis
Algebras, Groups and Geometries
Volume 31 • Number 3 • Page 293
September 1, 2014
Nathan O. Schmidt
In this preliminary work, we focus on a particular iso-geometrical, iso-topological facet of iso-mathematics
by suggesting a developing, generalized approach for encoding the states and transitions of spherically-symmetric
structures that vary in size. In particular, we introduce the notion of "effective iso-radius" to facilitate a
heightened characterization of dynamic iso-sphere Inopin holographic rings (IHR) as they undergo "iso-transitions"
between "iso-states". In essence, we propose the existence of "effective dynamic iso-sphere IHRs". In turn, this
emergence drives the construction of a new "effective iso-state" platform to encode the generalized dynamics of
such iso-complex, non-linear systems in a relatively straightforward approach of spherical-based iso-topic
liftings. The initial results of this analysis are significant because they lead to alternative modes of research
and application, and thereby pose the question: do these effective dynamic iso-sphere IHRs have application in
physics and chemistry? Our hypothesis is: yes. To answer this inquiry and assess this conjecture, this developing
work should be subjected to further scrutiny, collaboration, improvement, and hard work via the scientific method
in order to advance it as such.

Protium and Antiprotium in Riemannian Dual 4D Space-Time
Hadronic Journal
Volume 37 • Number 4 • Page 461
August 1, 2014
Nathan O. Schmidt Reza Katebi
In this preliminary paper, we apply the Riemannian dual (fractional quantum Hall superfluidic)
space-time topology and the six-coloring Gribov vacuum to protium and antiprotium. The results
suggest that it may be possible to generalize this framework to all atomic elements. Therefore,
this subject warrants further scrutiny, collaboration, refinement, and investigation.
Initiating the Effective Unification of Black Hole Horizon Area and Entropy Quantization with Quasi-Normal Modes
Advances in High Energy Physics
Volume 2014 • Article ID 530547
August 1, 2014
Christian Corda Seyed Hossein Hendi Reza Katebi Nathan O. Schmidt
Black hole (BH) area quantization may be the key to unlocking a unifying theory of quantum gravity (QG).
Surmounting evidence in the field of BH research continues to support a horizon (surface) area with a
discrete and uniformly spaced spectrum, but there is still no general agreement on the level spacing.
In the specialized and important BH case study, our objective is to report and examine the pertinent groundbreaking
work of the strictly thermal and nonstrictly thermal spectrum level spacing of the BH horizon area quantization with
included entropy calculations, which aims to tackle this gigantic problem. In particular, such work exemplifies a
series of imperative corrections that eventually permits a BH’s horizon area spectrum to be generalized from strictly
thermal to nonstrictly thermal with entropy results, thereby capturing multiple preceding developments by launching
an effective unification between them. Moreover, the results are significant because quasi-normal modes (QNM) and
"effective states" characterize the transitions between the established levels of the nonstrictly thermal spectrum.

Initiating Santilli's Iso-Mathematics to Triplex Numbers, Fractals, and Inopin's Holographic Ring: Preliminary Assessment and New Lemmas
Hadronic Journal
Volume 37 • Number 3 • Page 303
June 1, 2014
Nathan O. Schmidt Reza Katebi
In a preliminary assessment, we begin to apply Santilli's iso-mathematics to triplex numbers,
Euclidean triplex space, triplex fractals, and Inopin's 2-sphere holographic ring (HR) topology.
In doing so, we successfully identify and define iso-triplex numbers for iso-fractal geometry in a
Euclidean iso-triplex space that is iso-metrically equipped with an iso-2-sphere HR topology.
As a result, we state a series of lemmas that aim to characterize these emerging iso-mathematical structures.
These initial outcomes indicate that it may be feasible to engage this encoding framework to systematically
attack a broad range of problems in the disciplines of science and mathematics, but a thorough, rigorous,
and collaborative investigation should be in order to challenge, refine, upgrade, and implement these ideas.
Exterior and Interior Dynamic Iso-Sphere Holographic Rings with an Inverse Iso-Duality
Hadronic Journal
Volume 37 • Number 2 • Page 227
April 1, 2014
Nathan O. Schmidt
In this preliminary work, we use a dynamic iso-unit function to iso-topically lift the
"static" Inopin holographic ring (IHR) of the unit sphere to an interconnected pair of
"dynamic iso-sphere IHRs" (iso-DIHR), where the IHR is simultaneously iso-dual to both a
magnified "exterior iso-DIHR" and de-magnified "interior iso-DIHR". For both the
continuously-varying and discretely-varying cases, we define the dynamic iso-amplitude-radius
of one iso-DIHR as being equivalent to the dynamic iso-amplitude-curvature of its counterpart,
and conversely. These initial results support the hypothesis that a new IHR-based mode of
iso-geometry and iso-topology may be in order, which is significant because the interior
and exterior zones delineated by the IHR are fundamentally "iso-dual inverses" and may be
inferred from one another.
Initiating a Hypothetical Molecular Upgrade to Iso-Electronium with Topological Deformation Order
Parameters for Spontaneous Superfluidic Gauge Symmetry Breaking
April 1, 2014
Nathan O. Schmidt Reza Katebi Christian Corda
In this preliminary work, we propose a hypothesis and initiate a step-by-step, systematic upgrade
to the cutting-edge iso-electronium model by further equipping it with order parameters of
fractional statistics to encode the topological deformations, spontaneous superfluidic gauge
symmetry breaking, correlated helices with long range order, and wavepacket wavefunctions for
the toroidal polarizations. For this initial case, we consider the singlet planar coupling of
two hydrogen atoms that are interlocked with a Santilli-Shillady strong valence bond to form a
molecule with iso-electronium. The enhancement results support our hypothesis and are significant
because the order parameters arm the iso-electronium model an extra degree of freedom to work with,
which may authorize us to further decode and comprehend the underlying physical mechanisms and
features associated with the configuration of the toroidal polarizations. Thus, these outcomes
should be subjected to additional rigorous scrutiny and improvement via the scientific method.
Hawking Radiation — Quasi-Normal Modes Correspondence and Effective States for Nonextremal Reissner-Nordström Black Holes
Advances in High Energy Physics (Black Hole Special Issue)
Volume 2014 • Number 2 • Article ID 527874
February 11, 2014
Christian Corda Seyed Hossein Hendi Reza Katebi Nathan O. Schmidt
It is known that the nonstrictly thermal character of the Hawking radiation spectrum harmonizes
Hawking radiation with black hole (BH) quasi-normal modes (QNM).
This paramount issue has been recently analyzed in the framework of both Schwarzschild BHs (SBH) and Kerr BHs (KBH).
In this assignment, we generalize the analysis to the framework of nonextremal Reissner-Nordström BHs (RNBH).
Such a generalization is important because in both Schwarzschild and Kerr BHs an absorbed (emitted) particle has only mass.
Instead, in RNBHs the particle has charge as well as mass.
In doing so, we expose that, for the RNBH, QNMs can be naturally interpreted in terms of quantum levels for both particle
emission and absorption. Conjointly, we generalize some concepts concerning the RNBH's "effective states."
The Iso-Dual Tesseract
Algebras, Groups and Geometries
Volume 30 • Number 4 • Page 465
December 1, 2013
Nathan O. Schmidt
In this work, we deploy Santilli's iso-dual iso-topic lifting and Inopin's holographic ring (IHR) topology as a platform
to introduce and assemble a tesseract from two inter-locking, iso-morphic, iso-dual cubes in Euclidean triplex space.
For this, we prove that such an "iso-dual tesseract" can be constructed by following a procedure of simple, flexible,
topologically-preserving instructions. Moreover, these novel results are significant because the tesseract's state and
structure are directly inferred from the one initial cube (rather than two distinct cubes), which identifies a new iso-geometrical
inter-connection between Santilli's exterior and interior dynamical systems.
Dynamic Iso-Topic Lifting with Application to Fibonacci's Sequence and Mandelbrot's Set
Hadronic Journal
Volume 36 • Number 4 • Page 167
August 1, 2013
Nathan O. Schmidt
In this exploration, we introduce and define "dynamic iso-spaces", which are cutting-edge iso-mathematical constructions
that are built with "dynamic iso-topic liftings" for "dynamic iso-unit functions". For this, we consider both the continuous
and discrete cases. Subsequently, we engineer two simple examples that engage Fibonacci's sequence and Mandelbrot's set to
define a "Fibonacci dynamic iso-space" and a "Mandelbrot dynamic iso-space", respectively. In total, this array of resulting
iso-structures indicates that a new branch of iso-mathematics may be in order.
Effective State, Hawking Radiation and Quasi-Normal Modes for Kerr Black Holes
Journal of High Energy Physics
Volume 2013 • Number 8
June 4, 2013
Christian Corda Seyed Hossein Hendi Reza Katebi Nathan O. Schmidt
The non-strictly continuous character of the Hawking radiation spectrum generates a natural correspondence
between Hawking radiation and black hole (BH) quasi-normal modes (QNM). In this work, we generalize recent
results on this important issue to the framework of Kerr BHs (KBH). We show that also for the KBH, QNMs can
be naturally interpreted in terms of quantum levels. Thus, the emission or absorption of a particle is in
turn interpreted in terms of a transition between two different levels. At the end of the paper, we also
generalize some concepts concerning the "effective state" of a KBH.
Initiating the Newtonian Gravitational n-Body Spherical Simplification Algorithm on the Inopin Holographic Ring Topology
May 1, 2013
Nathan O. Schmidt
We propose a preliminary algorithm which is designed to reduce aspects of the n-body problem to a 2-body problem for
holographic principle compliance. The objective is to share an alternative view-point on the n-body problem to try and
generate a simpler solution in the future. The algorithm operates 2D and 3D data structures to initiate the encoding
of the chaotic dynamical system equipped with modified superfluid order parameter fields in both 3D and 4D versions
of the Inopin holographic ring (IHR) topology. For the algorithm, we arbitrarily select one point-mass to be the origin
and, from that reference frame, we subsequently engage a series of instructions to consolidate the residual (n-1)-bodies
to the IHR. Through a step-by-step example, we demonstrate that the algorithm yields "IHR effective" (IHRE) net
quantities that enable us to hypothetically define an IHRE potential, kinetic, and Lagrangian.
Mandelbrot Iso-Sets: Iso-Unit Impact Assessment
Hadronic Journal
Volume 36 • Number 2 • Page 211
April 1, 2013
Reza Katebi Nathan O. Schmidt
In this introductory work, we use Santilli's iso-topic lifting as a cutting-edge platform to explore Mandelbrot's set.
The objective is to upgrade Mandelbrot's complex quadratic polynomial with iso-multiplication and then computationally
probe the effects on this revolutionary fractal. For this, we define the "iso-complex quadratic polynomial" and engage
it to generate a locally iso-morphic array of "Mandelbrot iso-sets" by varying the iso-unit, where the connectedness
property is topologically preserved in each case. The iso-unit broadens and strengthens the chaotic analysis, and
authorizes an enhanced classification and demystification such complex systems because it equips us with an additional
degree of freedom: the new Mandelbrot iso-set array is an improvement over the traditional Mandelbrot set because it is
significantly more general. In total, the experimental results exemplify dynamic iso-spaces and indicate two modes of
topological effects: scale-deformation and boundary-deformation. Ultimately, these new and preliminary developments
spark further insight into the emerging realm of iso-fractals.
A Complex and Triplex Framework for Encoding the Riemannian Dual Space-Time Topology Equipped with Order Parameter Fields
Hadronic Journal
Volume 35 • Number 6 • Page 671
December 1, 2012
Nathan O. Schmidt
In this work, we forge a powerful, easy-to-visualize, flexible, consistent, and disciplined abstract vector framework for
particle and astro physics that is compliant with the holographic principle. We demonstrate that the structural
properties of the complex number and the sphere enable us to introduce and define the triplex number—an influential
information structure that is similar to the 3D hyper-complex number by D. White and P. Nylander—which identifies a
3D analogue of (2D) complex space. Consequently, we engage the complex and triplex numbers as abstract vectors to
systematically encode the state space of the Riemannian dual 3D and 4D space-time topologies, where space and time
are dual and interconnected; we use the triplex numbers (with triplex multiplication) to extend 1D and 2D algebraic
systems to 3D and 4D configurations. In doing so, we equip space-time with order parameter fields for topological
deformations. Finally, to exemplify our motivation, we provide three example applications for this framework.
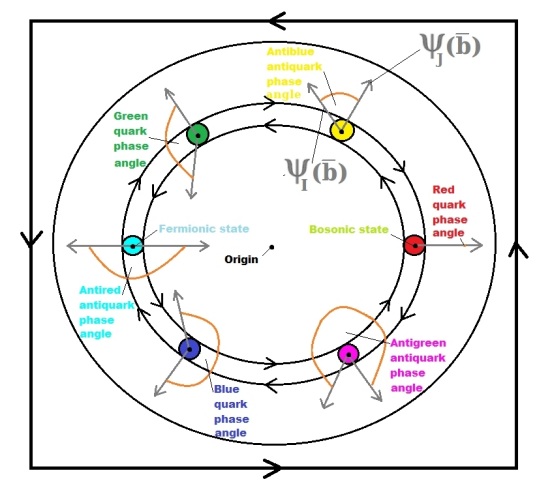
Proof of Quark Confinement and Baryon-Antibaryon Duality: I: Gauge Symmetry Breaking in Dual 4D Fractional Quantum Hall Superfluidic Space-Time
Hadronic Journal
Volume 35 • Number 5 • Page 469
October 1, 2012
Andrej E. Inopin Nathan O. Schmidt
We prove quark (and antiquark) confinement for a baryon-antibaryon pair and design a well-defined, easy-to-visualize, and
simplified mathematical framework for particle and astro physics based on experimental data. From scratch, we assemble
a dual 4D space-time topology and generalized coordinate system for the Schwarzschild metric. Space-time is equipped
with "fractional quantum number order parameter fields" and topological defects for the simultaneous and spontaneous
breaking of several symmetries, which are used to construct the baryon wavefunction and its corresponding antisymmetric
tensor. The confined baryon-antibaryon pair is directly connected to skyrmions with "massive 'Higgs-like' scalar amplitude-excitations"
and "massless Nambu-Goldstone pseudo-scalar phase-excitations". Newton's second law and Einstein's relativity are
combined to define a Lagrangian with effective potential and effective kinetic. We prove that our theory upgrades
the prediction precision and accuracy of QCD/QED and general relativity, implements 4D versions of string theory and
Witten's M-theory, and exemplifies M.C. Escher's duality.
On the k-Mer Frequency Spectra of Organism Genome and Proteome Sequences with a Preliminary Machine Learning Assessment of Prime Predictability
Boise State University Theses and Dissertations
Number 346
August 1, 2012
Nathan O. Schmidt
A regular expression and region-specific filtering system for biological records at the National Center for
Biotechnology database is integrated into an object-oriented sequence counting application, and a statistical
software suite is designed and deployed to interpret the resulting k-mer frequencies—with a priority focus on nullomers.
The proteome k-mer frequency spectra of ten model organisms and the genome k-mer frequency spectra of two bacteria and virus
strains for the coding and non-coding regions are comparatively scrutinized. We observe that the naturally-evolved
(NCBI/organism) and the artificially-biased (randomly-generated) sequences exhibit a clear deviation from the
artificially-unbiased (randomly-generated) histogram distributions. Furthermore, a preliminary assessment of
prime predictability is conducted on chronologically ordered NCBI genome snapshots over an 18-month period
using an artificial neural network; three distinct supervised machine learning algorithms are used to train
and test the system on customized NCBI data sets to forecast future prime states—revealing that, to a modest
degree, it is feasible to make such predictions.

Simulating Mobile Robots for Undergraduate Research
Journal of Computing Sciences in Colleges
Volume 23 • Issue 6 • Page 181
June 1, 2008
Suranga Hettiarachchi Eli Cohen Timothy Willey Nathan O. Schmidt
Our objective is to promote scientific research among undergraduate students at Eastern Oregon University
through the development of mobile robots. Simulating mobile robots in research is not a novel technique,
but using simulated robots that utilize virtual physics or "Physicomimetics" [2] as a tool to promote
undergraduate research is unique. This paper addresses the undergraduate research experience of designing
and implementing a simulated mobile robot environment using a physics-based control algorithm.